Aprendizaje por Refuerzo para Desarrolladores: Fundamentos y Q-Learning en la Práctica
Explora los conceptos esenciales del Aprendizaje por Refuerzo (RL) y sumérgete en una implementación práctica del algoritmo Q-Learning. Este artículo te proporcionará una base sólida para entender cómo los agentes de IA aprenden a tomar decisiones óptimas en entornos dinámicos.
Introducción al Aprendizaje por Refuerzo
El Aprendizaje por Refuerzo (RL) es una rama fascinante del Machine Learning que se inspira en cómo los seres vivos aprenden del entorno a través de la interacción y la retroalimentación. A diferencia del aprendizaje supervisado, que requiere datos etiquetados, o el no supervisado, que busca patrones en datos sin etiquetas, el RL permite a un agente aprender a tomar decisiones secuenciales para maximizar una recompensa acumulada a largo plazo en un entorno dinámico. [2, 5, 12]
Este paradigma es fundamental para desarrollar sistemas de IA capaces de operar en situaciones complejas y cambiantes, desde jugar videojuegos y controlar robots hasta optimizar procesos industriales y gestionar carteras de inversión. [6, 7, 9, 11]
En este artículo, desglosaremos los conceptos clave del Aprendizaje por Refuerzo y nos centraremos en uno de sus algoritmos más fundamentales y accesibles: el Q-Learning. Acompañaremos la teoría con un ejemplo práctico en Python para consolidar tu comprensión.
Conceptos Fundamentales del Aprendizaje por Refuerzo
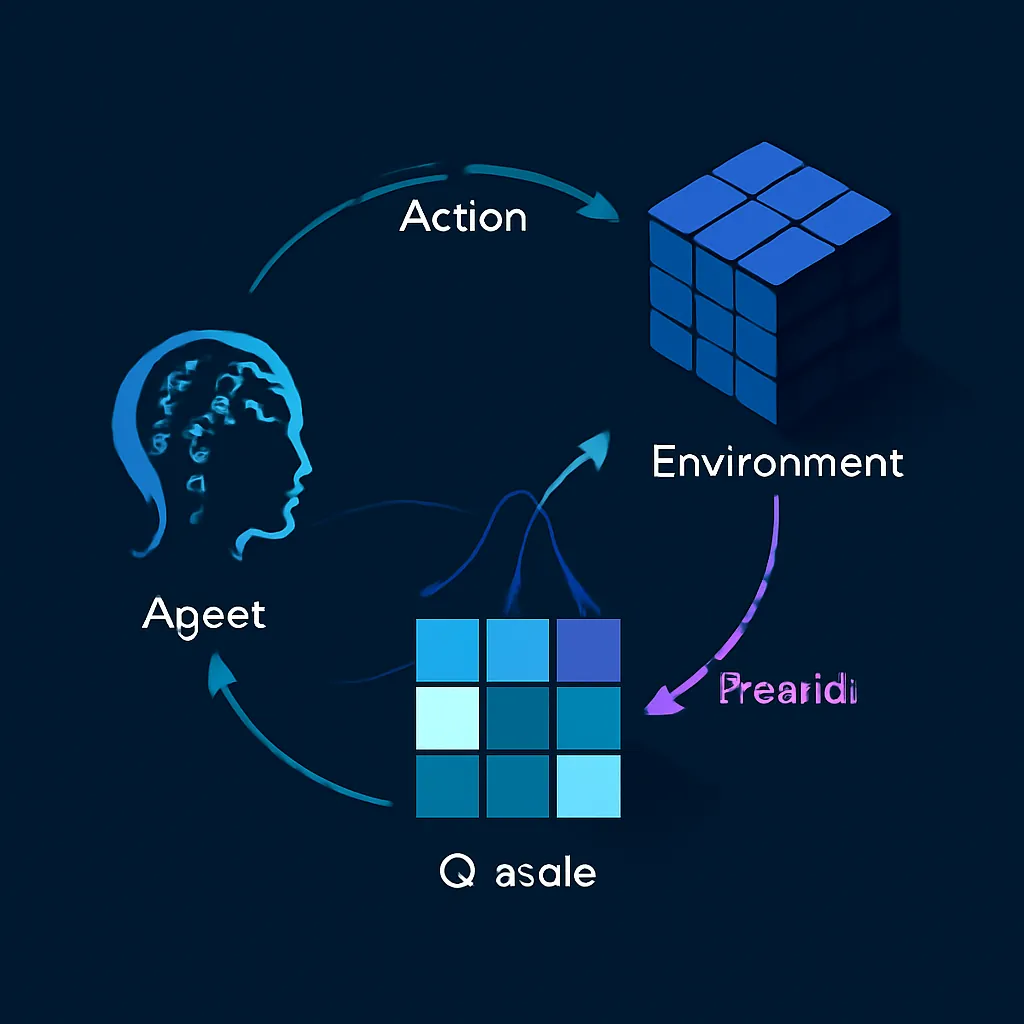
Para entender el RL, es crucial familiarizarse con sus componentes principales:
- Agente: Es la entidad que toma decisiones y aprende. Puede ser un programa de software, un robot, o cualquier sistema de IA. [2, 8]
- Entorno: Es el mundo con el que el agente interactúa. Define las reglas, los estados posibles y las recompensas asociadas a las acciones. [2, 8]
- Estado (State, S): Una representación de la situación actual del entorno en un momento dado. [2, 8, 17]
- Acción (Action, A): Un movimiento o decisión que el agente puede tomar en un estado particular. [2, 8, 17]
- Recompensa (Reward, R): Una señal numérica (positiva o negativa) que el entorno proporciona al agente después de realizar una acción. El objetivo del agente es maximizar la suma de recompensas a lo largo del tiempo. [2, 8, 17]
- Política (Policy, π): Define el comportamiento del agente, es decir, qué acción tomar en cada estado. Es la estrategia que el agente aprende. [2, 14]
- Función de Valor (Value Function): Estima la bondad de un estado o de una acción en un estado, en términos de la recompensa total esperada a largo plazo. Hay dos tipos principales:
- Función de Valor de Estado (V(s)): El valor esperado de empezar en un estado
sy seguir una políticaπ. - Función de Valor de Acción (Q(s, a)): El valor esperado de tomar la acción
aen el estadosy luego seguir una políticaπ. Esta es la base del Q-Learning. [3, 4, 17]
El proceso de aprendizaje en RL es iterativo: el agente observa el estado actual, toma una acción según su política, el entorno transiciona a un nuevo estado y proporciona una recompensa, y el agente utiliza esta retroalimentación para actualizar su política y sus funciones de valor. [2]
El Dilema Exploración-Explotación
Uno de los desafíos centrales en el Aprendizaje por Refuerzo es el dilema exploración-explotación. [2, 12]
- Exploración: El agente prueba nuevas acciones y estados para descubrir información potencialmente más gratificante sobre el entorno. Esto es crucial al principio para construir un conocimiento robusto.
- Explotación: El agente utiliza el conocimiento actual para tomar las acciones que ya sabe que le han proporcionado las mayores recompensas. Esto maximiza la recompensa a corto plazo.
Un agente debe equilibrar ambos para aprender de manera efectiva. Una estrategia común es la estrategia ε-greedy (epsilon-greedy), donde el agente elige una acción aleatoria (exploración) con una pequeña probabilidad ε (epsilon) y elige la mejor acción conocida (explotación) con probabilidad 1-ε. Con el tiempo, ε suele decrecer para que el agente explore menos y explote más a medida que su conocimiento mejora. [3, 19]
Q-Learning: Aprendizaje Basado en Valores
El Q-Learning es un algoritmo de Aprendizaje por Refuerzo sin modelo (no necesita conocer la dinámica del entorno) y off-policy (aprende la política óptima independientemente de la política que se esté siguiendo para explorar). Su objetivo es aprender la función de valor de acción óptima, Q*(s, a), que representa la máxima recompensa futura esperada al tomar la acción a en el estado s y luego actuar óptimamente. [1, 3, 4]
La Q-Table
El corazón del Q-Learning es la Q-Table (Tabla Q), una tabla que almacena los valores Q para cada par (estado, acción). Inicialmente, estos valores suelen ser cero o aleatorios. A medida que el agente interactúa con el entorno, la Q-Table se actualiza iterativamente. [3, 4, 17]
La Ecuación de Actualización de Q-Learning
La actualización de la Q-Table se basa en la Ecuación de Bellman, que relaciona el valor Q actual con el valor Q futuro máximo posible. [1, 3]
Q(s, a) ← Q(s, a) + α * [R + γ * max(Q(s', a')) - Q(s, a)]
Donde:
Q(s, a): El valor Q actual para el estadosy la accióna.α (alpha): La tasa de aprendizaje (learning rate), un valor entre 0 y 1 que determina cuánto de la nueva información se acepta. Un valor alto significa que el agente aprende rápidamente, pero puede ser inestable; un valor bajo significa un aprendizaje más lento pero más estable. [10, 15]R: La recompensa inmediata recibida después de tomar la acciónaen el estadosy transicionar al estados'. [15]γ (gamma): El factor de descuento (discount factor), un valor entre 0 y 1 que determina la importancia de las recompensas futuras. Un valor cercano a 0 hace que el agente se enfoque en recompensas inmediatas, mientras que un valor cercano a 1 le da más peso a las recompensas futuras.max(Q(s', a')): El valor Q máximo posible para el siguiente estados'sobre todas las posibles accionesa'. Esto representa la recompensa futura óptima que el agente espera obtener desde el nuevo estado.
Esta fórmula permite al agente ajustar sus estimaciones de valor Q basándose en la experiencia, acercándose gradualmente a la política óptima. [10]
Ejemplo Práctico: Q-Learning en un Entorno Simple (Grid World)
Para ilustrar el Q-Learning, implementaremos un agente que aprende a navegar en un entorno de cuadrícula simple (Grid World) para alcanzar un objetivo, evitando obstáculos.
Definición del Entorno
Imaginemos una cuadrícula de 4x4. El agente comienza en (0,0) y el objetivo está en (3,3). Hay un 'agujero' en (2,2) que da una penalización grande. Las acciones posibles son: arriba, abajo, izquierda, derecha.
- Recompensa por moverse: -1 (para fomentar caminos cortos).
- Recompensa por llegar al objetivo: +100.
- Recompensa por caer en el agujero: -100.
Implementación en Python
Necesitaremos NumPy para manejar la Q-Table y un bucle de entrenamiento.
import numpy as np
# 1. Definición del Entorno
# Representación del Grid World
# S: Start, G: Goal, H: Hole, F: Free
environment = np.array([
['S', 'F', 'F', 'F'],
['F', 'F', 'F', 'F'],
['F', 'F', 'H', 'F'],
['F', 'F', 'F', 'G']
])
# Mapeo de estados a índices numéricos
state_to_index = {(r, c): r * environment.shape[1] + c
for r in range(environment.shape[0])
for c in range(environment.shape[1])}
index_to_state = {v: k for k, v in state_to_index.items()}
num_states = environment.size
num_actions = 4 # 0: arriba, 1: abajo, 2: izquierda, 3: derecha
# Recompensas
rewards = np.full((num_states, num_actions), -1.0) # Costo por movimiento
# Recompensas especiales
goal_state_coords = (3, 3)
hole_state_coords = (2, 2)
goal_state_idx = state_to_index[goal_state_coords]
hole_state_idx = state_to_index[hole_state_coords]
# Recompensa por llegar al objetivo (desde cualquier acción que lleve a él)
for r in range(environment.shape[0]):
for c in range(environment.shape[1]):
current_state_idx = state_to_index[(r, c)]
# Acciones que llevan al objetivo
if r > 0 and state_to_index[(r-1, c)] == goal_state_idx: # Desde abajo
rewards[current_state_idx, 0] = 100.0
if r < environment.shape[0] - 1 and state_to_index[(r+1, c)] == goal_state_idx: # Desde arriba
rewards[current_state_idx, 1] = 100.0
if c > 0 and state_to_index[(r, c-1)] == goal_state_idx: # Desde derecha
rewards[current_state_idx, 3] = 100.0
if c < environment.shape[1] - 1 and state_to_index[(r, c+1)] == goal_state_idx: # Desde izquierda
rewards[current_state_idx, 2] = 100.0
# Penalización por caer en el agujero
for r in range(environment.shape[0]):
for c in range(environment.shape[1]):
current_state_idx = state_to_index[(r, c)]
# Acciones que llevan al agujero
if r > 0 and state_to_index[(r-1, c)] == hole_state_idx:
rewards[current_state_idx, 0] = -100.0
if r < environment.shape[0] - 1 and state_to_index[(r+1, c)] == hole_state_idx:
rewards[current_state_idx, 1] = -100.0
if c > 0 and state_to_index[(r, c-1)] == hole_state_idx:
rewards[current_state_idx, 3] = -100.0
if c < environment.shape[1] - 1 and state_to_index[(r, c+1)] == hole_state_idx:
rewards[current_state_idx, 2] = -100.0
# 2. Inicialización de la Q-Table
Q_table = np.zeros((num_states, num_actions))
# 3. Parámetros del Q-Learning
learning_rate = 0.8 # α
discount_factor = 0.95 # γ
epsilon = 1.0 # ε para la estrategia epsilon-greedy
epsilon_decay_rate = 0.001
num_episodes = 1000
# Función para obtener el siguiente estado y recompensa
def get_next_state_and_reward(current_state_idx, action):
r, c = index_to_state[current_state_idx]
next_r, next_c = r, c
if action == 0: # Arriba
next_r = max(0, r - 1)
elif action == 1: # Abajo
next_r = min(environment.shape[0] - 1, r + 1)
elif action == 2: # Izquierda
next_c = max(0, c - 1)
elif action == 3: # Derecha
next_c = min(environment.shape[1] - 1, c + 1)
next_state_idx = state_to_index[(next_r, next_c)]
reward = rewards[current_state_idx, action]
# Si la acción lleva a un estado terminal (goal o hole), la recompensa es directa
if next_state_idx == goal_state_idx:
reward = 100.0
elif next_state_idx == hole_state_idx:
reward = -100.0
return next_state_idx, reward
# 4. Bucle de Entrenamiento
for episode in range(num_episodes):
current_state_idx = state_to_index[(0, 0)] # Agente siempre empieza en (0,0)
done = False
while not done:
# Estrategia Epsilon-greedy para selección de acción
if np.random.uniform(0, 1) < epsilon:
action = np.random.randint(num_actions) # Exploración
else:
action = np.argmax(Q_table[current_state_idx, :]) # Explotación
# Obtener siguiente estado y recompensa
next_state_idx, reward = get_next_state_and_reward(current_state_idx, action)
# Actualizar Q-Table (Ecuación de Bellman)
old_q_value = Q_table[current_state_idx, action]
next_max_q = np.max(Q_table[next_state_idx, :])
new_q_value = old_q_value + learning_rate * (reward + discount_factor * next_max_q - old_q_value)
Q_table[current_state_idx, action] = new_q_value
current_state_idx = next_state_idx
# Condición de terminación del episodio
if current_state_idx == goal_state_idx or current_state_idx == hole_state_idx:
done = True
# Decaer epsilon
epsilon = max(0.01, epsilon - epsilon_decay_rate)
print("\nQ-Table final:\n", Q_table)
# 5. Probar la política aprendida
print("\nProbando la política aprendida:")
current_state_idx = state_to_index[(0, 0)]
path = [index_to_state[current_state_idx]]
total_reward = 0
while current_state_idx != goal_state_idx and current_state_idx != hole_state_idx:
action = np.argmax(Q_table[current_state_idx, :])
next_state_idx, reward = get_next_state_and_reward(current_state_idx, action)
total_reward += reward
current_state_idx = next_state_idx
path.append(index_to_state[current_state_idx])
if len(path) > 20: # Evitar bucles infinitos en caso de mala convergencia
print("Ruta demasiado larga, posible bucle.")
break
print("Ruta encontrada:", path)
print("Recompensa total obtenida:", total_reward)
Este código simula el aprendizaje de un agente en el Grid World. La Q-Table se inicializa con ceros y, a lo largo de miles de episodios, el agente explora el entorno y actualiza los valores Q. Con el tiempo, los valores Q convergen, indicando las mejores acciones a tomar en cada estado para maximizar la recompensa. [13, 16]
Aplicaciones del Aprendizaje por Refuerzo en el Mundo Real
El Aprendizaje por Refuerzo ha demostrado ser increíblemente potente en una variedad de dominios:
- Juegos: Desde el famoso AlphaGo de DeepMind, que venció al campeón mundial de Go, hasta agentes que dominan videojuegos complejos como Dota 2 o StarCraft II. [7, 12]
- Robótica: Permite a los robots aprender a realizar tareas complejas, como manipular objetos, caminar o navegar en entornos desconocidos, a través de la interacción y la retroalimentación. [7, 11]
- Vehículos Autónomos: Ayuda a los coches sin conductor a tomar decisiones en tiempo real, como cambiar de carril, frenar o acelerar, basándose en las condiciones del tráfico y el entorno. [11]
- Sistemas de Recomendación: Puede personalizar las sugerencias para los usuarios, aprendiendo de sus interacciones y preferencias a lo largo del tiempo. [2]
- Optimización de Procesos: Utilizado en la gestión de inventarios, optimización de rutas de transporte, planificación de la producción y control de sistemas complejos. [9]
- Finanzas: Desarrollo de agentes de trading que aprenden estrategias de inversión óptimas. [19]
Desafíos y Futuro del RL
A pesar de su potencial, el RL presenta desafíos significativos:
- Eficiencia de Datos: A menudo requiere una gran cantidad de interacciones con el entorno para aprender, lo que puede ser costoso o lento en entornos reales.
- Diseño de Recompensas: Definir una función de recompensa adecuada que guíe al agente hacia el comportamiento deseado puede ser complejo.
- Estabilidad y Convergencia: Garantizar que los algoritmos de RL converjan a una política óptima de manera estable puede ser difícil, especialmente en entornos complejos.
El futuro del RL se encamina hacia el Deep Reinforcement Learning (DRL), que combina el RL con redes neuronales profundas para manejar estados y acciones de alta dimensionalidad, abriendo la puerta a aplicaciones aún más sofisticadas. [2, 18]
Conclusión
El Aprendizaje por Refuerzo es un campo vibrante y en constante evolución de la Inteligencia Artificial que ofrece un enfoque poderoso para la toma de decisiones autónoma. Comprender sus fundamentos y algoritmos como el Q-Learning es un paso esencial para cualquier desarrollador o profesional técnico que busque construir sistemas de IA capaces de aprender y adaptarse en entornos complejos. Con la continua investigación y el avance de la capacidad computacional, el RL seguirá transformando la forma en que interactuamos con la tecnología y resolvemos problemas del mundo real.
